EJEMPLO 1. Concepto de probabilidad
En él, se tirará 15, 30 y 100 veces la moneda y se verá como tiende el valor de la frecuencia relativa. ¿Qué diferencias hay?, ¿es igual tirar 15, 30 ó 100 veces la moneda?, ¿a qué valor tiende la frecuencia relativa?
EJEMPLO 2. Representación de la frecuencia relativa en forma de histogramas
Se utilizarán los datos del ejemplo de la concentración de nitratos:
Resultados de la concentración de nitratos en agua (μg L-1)
| ||||||||
0,51
|
0,50
|
0,50
|
0,50
|
0,50
|
0,49
|
0,52
|
0,50
|
0,47
|
0,51
|
0,52
|
0,53
|
0,48
|
0,49
|
0,50
|
0,52
|
0,49
|
0,50
|
0,49
|
0,48
|
0,46
|
0,49
|
0,49
|
0,48
|
0,49
|
0,51
|
0,47
|
0,50
|
0,51
|
0,51
|
0,48
|
0,48
|
0,47
|
0,50
|
0,49
|
0,48
|
0,50
|
0,50
|
0,50
|
0,53
|
0,53
|
0,52
|
0,50
|
0,51
|
0,51
|
Ejemplo sacado de Miller y Miller (2009).
EJEMPLO 3. Cálculos de los Estadísticos más importantes
Para eso usaremos los datos de la concentración de nitratos del Ejemplo 2
EJEMPLO 4. Cálculo del intervalo de confianza
Usando los estadísticos del Ejemplo 3, calcularemos el intervalo de confianza para el análisis de la concentración de nitratos al 90, 95 y 99% de confianza.
EJEMPLO 5. Cálculo de la propagación de errores
Imaginemos el siguiente ejemplo:
Queremos saber la cantidad total de una sustancia química A que hemos extraído de una muestra de biológica. Para lo cual, hacemos dos submuestras y realizamos dos extracciones obteniendo en la primera 46,59 ± 2,12 mg y en la segunda, 15,24 ± 1,01 mg respectivamente. ¿Cuál es la cantidad total obtenida con un 95% de confianza?
Nota: media ± desviación estándar. El número de repeticiones en cada extracción es de 5.
EJEMPLO 6. Contraste de hipótesis
Imaginemos que hemos analizado las muestras de agua del río que pasa por al lado de una granja. Hemos obtenido un valor de 54,3 ± 5,2 mg L-1 al medir 20 muestras. Queremos saber si hay contaminación por nitratos en una muestra de agua de un rio (Nota: se considera que existe cuando es distinto significativamente de 50 mg L-1, acorde con la legislación vigente)
Planteamos las siguientes hipótesis:
- H0: El valor de nuestros análisis es igual a 50 mg L-1
- H1: El valor de nuestros análisis es mayor a 50 mg L-1
Repetir este ejercicio con 51,3 ± 5,2 mg L-1. ¿Existe contaminación?
Recordatorio: descartaremos H0 si p-valor ≤ α, siendo α = 0,05, (también puede ser 0,01 y 0,001).
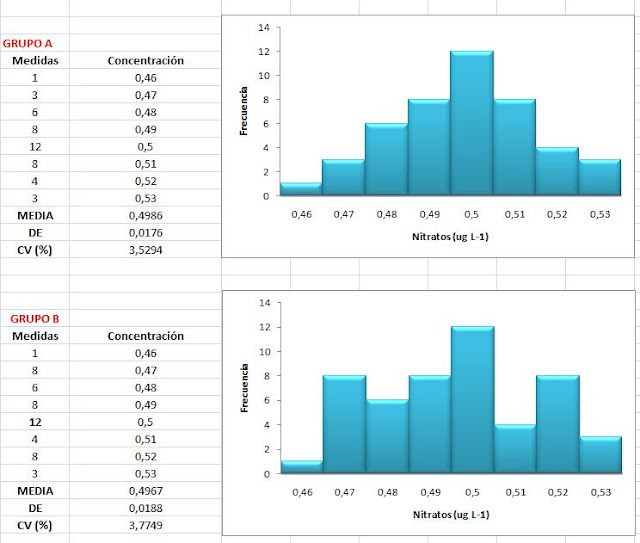
EJEMPLO 7. Test de Normalidad.
Vamos a realizar un test de Normalidad a dos grupos de datos:
| GRUPO A | |
| Medidas | Concentración |
| 1 | 0,46 |
| 3 | 0,47 |
| 6 | 0,48 |
| 8 | 0,49 |
| 12 | 0,5 |
| 8 | 0,51 |
| 4 | 0,52 |
| 3 | 0,53 |
| MEDIA | 0,4986 |
| DE | 0,0176 |
| CV (%) | 3,5294 |
| GRUPO B | |
| Medidas | Concentración |
| 1 | 0,46 |
| 8 | 0,47 |
| 6 | 0,48 |
| 8 | 0,49 |
| 12 | 0,5 |
| 4 | 0,51 |
| 8 | 0,52 |
| 3 | 0,53 |
| MEDIA | 0,4967 |
| DE | 0,0188 |
| CV (%) | 3,7749 |
Contrastes de la media de una población con un valor de referencia.
Vamos a comparar los dos grupos de datos del Ejemplo 7 para saber si son diferentes estadísticamente del valor de referencia de 0,54 μg L-1. Utilizaremos el test paramétrico o no paramétrico en función de como haya salido Test de Normalidad.
EJEMPLO 8.1. t de Student, (paramétrico)
EJEMPLO 8.2. Tests de signos (no paramétrico)
Para lo cual, deberemos calcular la diferencia de cada valor con respecto al de referencia y obtener el signo (negativo si es menor y positivo si en mayor). En nuestro caso, las 50 serían positivas.
Comparación entre dos muestras poblacionales.
Compararemos dos muestras poblacionales en el caso de que sean normalizadas e independientes:
A: 255,24 ± 2,01 mg
B: 307,14 ± 3,78 mg
Nota: media ± desviación estándar. El número de repeticiones en cada extracción es de 10.
EJEMPLO 9.1. t de Student, (paramétrico)
Compararemos dos muestras poblacionales en el caso de que sean normalizadas e independientes:
A: 255,24 ± 2,01 mg
B: 307,14 ± 3,78 mg
Nota: media ± desviación estándar. El número de repeticiones en cada extracción es de 10.
EJEMPLO 9.2. U de Mann-Whitney (no paramétrico).
Comparación entre más dos muestras poblacionales.
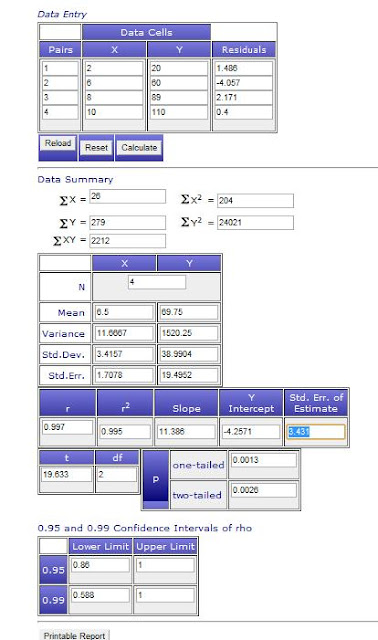
EJEMPLO 10.1. Análisis de la Varianza (paramétrico).
Para eso, utilizaremos la hoja de excel disponible en: http://www.amstat.org/publications/jse/v18n2/ANOVAExercise.xls
Compararemos dos muestras poblacionales en el caso de que sean normalizadas e independientes:
Group
|
group 1
|
group 2
|
group 3
|
group 4
|
group 5
|
12
|
2
|
60
|
5
|
50
| |
13
|
2
|
65
|
3
|
56
| |
14
|
10
|
68
|
6
|
54
| |
15
|
9
|
67
|
10
|
53
| |
12
|
5
|
59
|
10
|
57
| |
13
|
7
|
58
|
5
|
58
| |
14
|
1
|
63
|
8
|
59
| |
15
|
7
|
61
|
6
|
56
| |
12
|
5
|
60
|
7
|
58
| |
14
|
1
|
62
|
3
|
54
| |
15
|
4
|
63
|
7
|
57
| |
10
|
6
|
68
|
4
|
58
| |
10
|
9
|
94
|
2
|
59
| |
10
|
5
|
89
|
3
|
56
| |
11
|
2
|
87
|
7
|
54
| |
12
|
2
|
86
|
5
|
53
| |
17
|
7
|
94
|
5
|
52
| |
13
|
5
|
98
|
3
|
56
| |
14
|
4
|
91
|
4
|
58
| |
15
|
8
|
93
|
9
|
54
| |
Average
|
13,05
|
5,01
|
74,30
|
5,44
|
55,60
|
Sum
|
261
|
100
|
1486
|
109
|
1112
|
Std_Dev
|
1,93
|
2,78
|
14,85
|
2,32
|
2,50
|
Count
|
20,00
|
20,00
|
20,00
|
20,00
|
20,00
|
Std_Error
|
0,43
|
0,62
|
3,32
|
0,52
|
0,56
|


0 comentarios:
Publicar un comentario